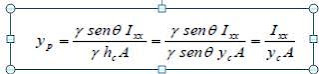C 05 FUERZAS HIDROSTÁTICAS SOBRE UNA SUPERFICIE PLANA SUMERGIDA

C 05 FUERZAS HIDROSTÁTICAS SOBRE UNA SUPERFICIE PLANA SUMERGIDA

Puesto que no puede haber esfuerzos de corte en un fluido estático, todas las fuerzas hidrostáticas que actúan sobre una superficie sumergida en dicho fluido deberán ser normales (perpendiculares) a la misma.

Si la presión se distribuye uniformemente sobre un área, como se muestra en la Figura 1.a, la fuerza es igual a la presión por el área, y el punto de aplicación de la fuerza es el centroide del área.

En el caso de líquidos, la distribución de la presión no es uniforme; de aquí que es necesario un análisis más amplio. Considere una superficie plana vertical, como la que se muestra en la Figura 1.b, cuyo extremo superior coincide con la superficie libre del líquido. La presión variará desde cero en M, hasta NK en N. Así, la fuerza total sobre un lado es la sumatoria de los productos de los elementos de área por la presión sobre ellos. Es claro que la resultante de este sistema de fuerzas paralelas deberá estar aplicada en un punto por abajo del centroide del área, ya que el centroide de un área es el punto de aplicación de la resultante de un sistema de fuerzas paralelas uniformes.

          P = F / A   

Luego:     F = P * A

Si la superficie se sumerge hasta la posición M’N’ mostrada en la Figura 1.c, el cambio proporcional de presión de M’ a N’ es menor que el de M a N. De aquí que el centro de presión estará más cercano al centroide de la superficie. Entre más se sumerja la superficie, la presión sobre ésta llegará a ser más uniforme y el centro de presión estará cada vez más cerca del centroide.

                     

La Figura 2 muestra una superficie plana de forma arbitraria sumergida completamente en un líquido, la cual forma un ángulo θ con la horizontal. A la derecha se muestra la proyección de esta superficie sobre un plano vertical. Sea h la profundidad de cualquier punto y y la distancia del punto a la superficie libre en el plano de la placa.

Considere un elemento de área seleccionado de manera que la presión ejercida sobre él es uniforme. Si x representa el ancho del área a cualquier profundidad.

Si se representa mediante hc la profundidad del centroide, entonces:

h_c = y_{c *} sen θ 

                              F =h_{c *} A _* γ                                (A)

Ya que γ _* hc  es la presión en el centroide, la Ec.(A) indica que la fuerza sobre una cara de cualquier superficie plana sumergida en un fluido estático, es igual a la presión que hay en el centroide de dicha cara por su área, independientemente de la forma de la superficie y de su ángulo de inclinación.

CENTRO DE PRESIÓN

Para completar el análisis de fuerzas planas, se debe determinar el punto de aplicación de la fuerza resultante. Este punto se denomina centro de presión.

Tomando el eje x de la Figura 2,  se tiene:

                   

(B)

El teorema de los ejes paralelos para momentos de inercia establece que

I_xx = I_cg + y_c ² _*  A

donde Icg es el momento de inercia del área con respecto a un eje paralelo al eje x (cg) que pasa a través del centro del área. Con esto, la Ec.(B) se puede escribir como:

De esta ecuación, se puede observar que el centro de presión es independiente del ángulo θ. También, se puede ver que el centro de presión siempre está por abajo del centroide y que, cuando la profundidad del centroide se incrementa, el centro de presión se aproxima al centroide.

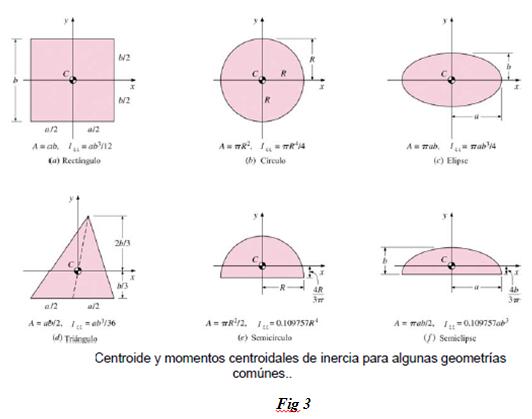
En la Figura 3 se dan los valores de Icg para algunas áreas comunes.

Para determinar la posición lateral del centro de presión, considérese la vista normalA-A de la Figura 2, que se muestra en la Figura 4.

El centro de presión se muestra en la posición yp, determinada previamente, y a una distancia desconocida xp del eje y. Igualando el momento alrededor del eje y de la fuerza resultante con el momento correspondiente de la distribución de presión, se obtiene:

donde Ixy es el producto de inercia alrededor de los ejes de referencia. Empleando el teorema de los ejes paralelos para el producto de inercia:

donde Ixy es el producto de inercia con respecto a los ejes cetroidales, se obtiene

Un modo fácil de calcular x_p es fijar el sistema de ejes coordenados xy, de tal manera que el eje y pase a través del centroide del área y x = 0 esté en el centroide. Si el área es simétrica en relación con cualquiera de los ejes, el producto de inercia en el centroide es cero, y xp coincide con el centroide.

FORMULAS PARA DETERMINAR LA FUERZA DE EMPUJE SOBRE SUPERFICIES PLANAS VERTICALES SUMERGIDAS

ECUACIÓN GENERAL

E = g * Sen q * y_g * A

ECUACIÓN PARTICULAR

E = g * b * h² / 2

          

Donde:

E = Fuerza de empuje del fluido en N, kp, Lb, kgf.

g = Peso específico en (kp / dm³) , (Ton / m³).

b = Ancho de la compuerta en cm, dm, m.

h = Altura sumergida de la compuerta o elemento sumergido en cm, dm, m.

y_g = Altura desde el espejo de agua, hasta la aplicación de la fuerza de empuje E.